Cómo funcionan los algoritmos de compresión de vídeo
A raíz de un post del recién estrenado blog de Gin (en el momento que empecé a escribir el artículo), en el que para explicar el porqué de los diferentes tamaños de los ficheros en los capítulos de anime de Backbeard así como las mejoras que suponen los Ordered Chapters externos de los mkv, hace una pequeña explicación de cómo funcionan los algoritmos de compresión de vídeo. Me he animado a realizar un documento un poco más técnico explicando cómo funcionan realmente estos algoritmos.
Además, si consigo que entendais cómo funcionan descubrireis el porqué de muchos de los efectos que aparecen en los videos cuando se emplea un bitrate muy bajo, como pueden ser los temidos «macrobloques» o el asqueroso «banding».
Compresión de imagen estática
En primer lugar, hay que conocer cómo se comprime actualmente una imagen estática (uséase una foto). En este caso, y como nos interesa para el funcionamiento de los codecs de vídeo explicaré JPEG (sí, por fin sabreis porqué vuestra cara parece una mancha rosa cuando poneis el nivel de compresión al máximo xD).
Básicamente, dejando aparte conversiones de color RGB <-> YCbCr (que ese es otro tema) el algoritmo JPEG original funciona de la siguiente forma.
División
Divide la imagen en trocitos más pequeños y manejables (como la del marido de la morena). En este caso en cuadros de píxeles de 8×8, es decir, 8 píxeles de ancho y 8 píxeles de alto, por lo que cada trocito dispone de un total de 64 píxeles.
Henge no Jutsu!! (Transformación)
A cada trocito le aplica una transformada matemática conocida como DCT (transformada de coseno discreta).
Esta operación matemática tiene diversas propiedades (que no voy a explicar), pero a nosotros nos importan dos principalmente.
La primera de ellas es que es reversible, vamos que podemos volver a obtener la imagen original otra vez. Y la segunda es que «compacta muy bien la energía» de las imágenes.
En esta imagen se puede observar lo que consigue.
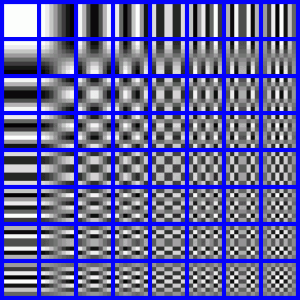
Transformada discreta del coseno
Resumiendo, en la primera casilla (esquina superior izquierda) sacaría algo así como el color medio del cuadro, luego conforme nos movemos hacia la derecha se puede ver la variación de frecuencia en vertical y hacia abajo en horizontal. Los cuadros restantes son la combinación de las casillas de la fila y la columna correspondiente.
Esto, en términos visuales se traduce en que cuanto más a la derecha o más abajo de la matriz, más rápida es la variación de color existente. Es decir, si todos los colores del cuadro son muy parecidos, casi toda la energía estará concentrada en los primeros cuadros de la matriz. Sin embargo, si existe un cambio brusco de color (como puede suceder entre dos baldosas en un tablero de ajedrez) la energía suele estar situada en las frecuencias altas, ya que el cambio de color es muy brusco.
A recortar! (Cuantización)
Una vez se ha transformado la imagen, lo que se hace es eliminar los datos molestos. Para ello se aplica un proceso llamado cuantización. Es decir, aquí, a mi modo de ver, es donde realmente se realiza el proceso de compresión en JPEG.
Imaginemos que tras la transformación de la imagen disponemos de una matriz tal que así (Hago la matriz de 4×4 para no trabajar tanto).
| 200 | 102 | 7 | 3 |
| 103 | 101 | 4 | 2 |
| 11 | 2 | 0 | 0 |
| 3 | 0 | 0 | 15 |
Vaya, cuánto cero al final… y cuántos números bajitos… ¿se podría hacer algo para quitar lo qué molesta? De hecho sí… y se hace.
A este paso se le llama cuantización. Lo que se hace es dividir cada casilla de la matriz por un valor determinado para conseguir hacer los números más bajitos. en este caso (por ejemplo) usaremos la siguiente matriz (la llamaremos matriz de cuantización):
| 2 | 4 | 8 | 16 |
| 4 | 4 | 8 | 16 |
| 8 | 8 | 8 | 16 |
| 16 | 16 | 16 | 16 |
Si os fijais, los valores más altos se encuentran en los extremos de la matriz. Si realizamos la división, la matriz original se convierte en esta:
| 100 | 25 | 0 | 0 |
| 25 | 25 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
¡Maravilla! ¡Y se hicieron los ceros!
¿Qué conseguimos haciendo ceros? Lo explicaré en el siguiente punto.
Ahora lo que estais pensando es que la matriz no se parece en nada a la original. Efectivamente, sin embargo si la volvemos a multiplicar por la matriz de cuantización, se obtiene una matriz muy parecida a la original, pero que evidentemente no es igual, por lo que aquí es donde se tienen las pérdidas, lo que hace que una imagen comprimida con jpeg pierda información respecto a un png o un bmp.
Último paso (Y se hizo el algoritmo)
Por último, se recorre la matriz en forma de zig-zag (ahora no recuerdo ezactamente como), pero imaginemos que se empieza en el 100 hacia la derecha, luego en diagonal hacia el 25 que hay debajo del 100, luego al 1 que hay bajo el 25 y se vuelve a subir por la diagonal pasando por el 25 y el 0, por último se recorren el resto de ceros.
Si lo ponemos en línea y contando los números que son iguales obtendriamos algo así: «1-100 2-25 1-1 1-25 11-0» (A este método de compresión se le conoce como Run Lenght Encoding). Si lo comparamos con el bloque original, (antes de cuantización) podemos ver como es sensiblemente más corto «1-200 1-102 1-103 1-11 1-101 1-7 1-3 1-4 1-2 1-3 2-0 1-2 1-0 1-15» evidentemente se ha perdido información. Sin embargo lo importante, sigue relativamente igual.
Por último se aplica un tipo de compresión conocida como Huffman para reducir en lo posible el tamaño de la imagen.
Explicación de efectos
Espero que con esta pequeña explicación hayais podido entender el porqué de los cuadrados que aparecen en las imágenes JPEG, ya que cada cuadrado es un bloque de 8×8 donde se ha aplicado este algoritmo, además si os fijais al emplear una imagen jpeg se suele poder apreciar la división entre bloques ya que son cuadrados de un color muy parecido (pero no igual).
Además, como en JPEG se suelen eliminar las frecuencias altas (cambios bruscos de color) se desaconseja bastante para texto de hecho no se aconseja en absoluto xD.
La explicación de cómo afecta esto a los vídeos, será en otro artículo, basado en este, que espero que disfruteis pronto.
Evidentemente me he dejado muchas cositas en el tintero y no he sido todo lo preciso que se podría esperar (correcciones son bienvenidas) pero espero que los que no teneis casi idea de compresión de video/imágenes hayais podido entender un poco los principios de este tema.
Saludos a todos.
Como en el anterior artículo, por si acaso, le pongo copyleft a este artículo, el menos restrictivo posible, pero al menos citadme. (Batousay – http://www.batousay.com)
La imagen ha sudo obtenida de la Wikimedia (http://commons.wikimedia.org/wiki/File:DCT-8×8.png) By Devcore (Own work) [Public domain], via Wikimedia Commons
Los demás conocimientos son mios (obtenidos en un par de asignaturas de la carrera), aunque he refrescado un poco la memoria con la Wikipedia.
¿Te gusta este post? ¡Compártelo!
3 Comentarios
21:28 pm
Muy interesante y muy bien explicado Batousay, te ánimo a que continúes explicando cositas de estas, personalmente estoy muy interesado en todo lo que tenga que ver con el encodeo.
P.S.: Como dices que te digamos cualquier fallo, he visto un par de fallitos tontos, dos tildes innecesarias en la ‘a’ de ‘imagen’ que se te han escapado, y también la falta de exclamación inicial en otro uno de los títulos (aunque esta a lo mejor la has puesto a próposito xD). Y perdona si no eran estás las correcciones a las que te referías ^^’
22:55 pm
Tildes corregidos, ¡muchas gracias!.
La exclamación inicial es a posta xD.
Y sí, me refería a cualquier tipo de corrección, gracias.
En cuanto a la continuación del post… en ello estoy, el problema es mi falta de tiempo. Pero bueno, en cuanto acabe un par de proyectos del fansub continuaré con este tutorial…
Saludos
Debes de estar logueado para dejar un comentario.
« Compresión de Bluray en Ubuntu (GNU/Linux based) Cómo pasarlos a MKV Siguiente post
Aviso sonoro de CAPTCHA para jDownloader en Linux »





15:07 pm
¡Muy bien resumido! Precisamente ayer pensaba en redactar algo más sobre encodeo en el blog. Probablemente lo haga hoy si me animo.
A ver como sigues, que al final tendremos una ewiki del x264 versión Batu. xD